Travelling-wave-induced flows unveil a fascinating world where the rhythmic motion of waves generates complex fluid dynamics. This phenomenon, observed across diverse scales from microscopic channels to vast oceans, presents a rich tapestry of scientific inquiry. We’ll explore the underlying mechanisms, mathematical models, experimental techniques, and real-world applications of these intriguing flows.
From the elegant mathematics governing their behavior to the practical applications shaping various fields, understanding travelling-wave-induced flows requires a multidisciplinary approach. This exploration delves into the fundamental physics, offering a comprehensive overview of current knowledge and future research directions.
Introduction to Travelling-Wave-Induced Flows
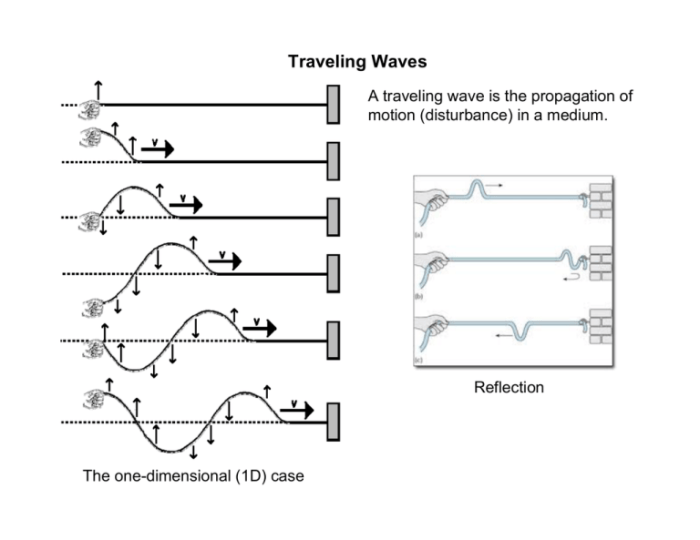
Travelling-wave-induced flows describe the movement of fluids – liquids or gases – caused by the propagation of waves through the fluid or along a boundary interacting with it. These flows are ubiquitous in nature and engineering applications, arising from various wave types and mechanisms. Understanding these flows is crucial across multiple scientific disciplines.Travelling-wave-induced flows are fundamentally driven by the transfer of momentum from the wave to the fluid.
This momentum transfer can occur through several mechanisms, including pressure gradients generated by the wave, shear stresses due to wave-induced boundary layer effects, or even direct interactions between the wave and suspended particles within the fluid. The resulting flow can be complex, ranging from simple unidirectional currents to intricate three-dimensional patterns. The precise nature of the flow depends heavily on the characteristics of the wave itself (e.g., amplitude, frequency, wavelength) and the properties of the fluid (e.g., viscosity, density).
The Importance of Studying Travelling-Wave-Induced Flows
The study of travelling-wave-induced flows is significant across various fields. In oceanography, understanding wave-driven currents is crucial for predicting coastal erosion, sediment transport, and the dispersion of pollutants. In biophysics, travelling waves are essential in understanding processes like blood flow in arteries (where pressure waves induce flow) and the movement of cilia in biological systems. In chemical engineering, wave-induced mixing in reactors can be optimized to improve reaction rates and product yield.
In geophysical fluid dynamics, the study of travelling waves is crucial for understanding atmospheric and oceanic circulation patterns and the associated weather phenomena. Furthermore, the interaction of waves with structures is of paramount importance in designing robust coastal and offshore engineering infrastructure.
Types of Travelling Waves and Associated Flow Characteristics
The following table summarizes different types of travelling waves and their associated flow characteristics. Note that the flow characteristics can be significantly influenced by factors like wave amplitude, fluid properties, and boundary conditions.
| Wave Type | Mechanism | Flow Characteristics | Example |
|---|---|---|---|
| Surface Gravity Waves (Ocean Waves) | Pressure gradients, shear stresses | Orbital motion near the surface, net mass transport in the direction of wave propagation (Stokes drift), boundary layer effects near the seabed. | Ocean currents generated by wind-driven waves |
| Internal Gravity Waves (Ocean Waves) | Density stratification, buoyancy forces | Oscillatory flows within stratified layers, potential energy conversion to kinetic energy. | Internal waves in the ocean thermocline |
| Acoustic Waves | Pressure fluctuations | Compressional flow, typically weak unless very high intensity | Acoustic streaming in fluids due to high-intensity sound |
| Solitary Waves (e.g., Solitons) | Nonlinear wave dynamics | Localized wave packets, can propagate without significant dispersion. | Tsunami waves (approximated as solitons) |
Mathematical Modeling of Travelling-Wave-Induced Flows
Modeling travelling-wave-induced flows requires a careful consideration of the fluid dynamics involved. The complexity of the model depends heavily on the specific application and the level of detail required. Simpler models offer computational efficiency, while more complex models strive for higher accuracy.
The choice of governing equations is crucial. For many scenarios, the Navier-Stokes equations provide a robust framework. These equations describe the conservation of mass and momentum in a fluid, accounting for viscous effects. However, the Navier-Stokes equations are notoriously difficult to solve analytically, except for very simplified cases. Therefore, numerical methods are almost always necessary.
Governing Equations and Assumptions, Travelling-wave-induced flows
The Navier-Stokes equations, in their full form, are rarely used directly for modeling travelling-wave-induced flows due to their computational cost. Significant simplifications and assumptions are often made to make the problem tractable. Common simplifications include assuming incompressibility (constant density), neglecting certain terms in the equations based on scale analysis (e.g., neglecting the advective terms compared to the diffusive terms in certain flow regimes), or using a shallow water approximation.
The shallow water equations, for example, are a simplified set of equations applicable when the vertical length scale of the flow is much smaller than the horizontal length scale. This assumption reduces the dimensionality of the problem and simplifies the governing equations significantly. Other simplifications might involve assuming a specific wave profile (e.g., sinusoidal) or neglecting certain boundary conditions to simplify the geometry.
The validity of these assumptions must be carefully evaluated for each specific application.
Numerical Methods for Solving the Equations
Several numerical methods are available for solving the governing equations, each with its own strengths and weaknesses. The Finite Difference Method (FDM) is a relatively straightforward approach where the derivatives in the governing equations are approximated using difference quotients at discrete grid points. FDM is often computationally efficient but can struggle with complex geometries. The Finite Element Method (FEM) offers greater flexibility in handling complex geometries and boundary conditions.
FEM divides the domain into smaller elements, solving the equations locally on each element and then assembling the solutions. While FEM is more versatile, it is generally more computationally expensive than FDM. Other methods, such as spectral methods or boundary element methods, may also be suitable depending on the specific problem characteristics. The choice of method often depends on a balance between accuracy, computational cost, and the complexity of the geometry and boundary conditions.
Simplified Model for a Specific Flow
Let’s consider a simplified model for a travelling wave inducing flow in a long, narrow channel. We assume a shallow water approximation, a sinusoidal wave profile, and a constant water depth. We can use the one-dimensional shallow water equations:
∂h/∂t + ∂(hu)/∂x = 0 (Conservation of mass)
∂(hu)/∂t + ∂(hu2 + 1/2gh 2)/∂x = -gh∂η/∂x (Conservation of momentum)
where:* h is the water depth,
- u is the flow velocity,
- g is the acceleration due to gravity,
- η is the wave elevation (η = A sin(kx – ωt), where A is the wave amplitude, k is the wave number, and ω is the angular frequency).
These equations can be solved numerically using methods like FDM or a simple explicit scheme. The parameters A, k, ω, and the channel geometry would need to be specified based on the specific physical situation. Boundary conditions would need to be defined at the channel ends (e.g., reflecting or absorbing boundaries). This simplified model provides a starting point for investigating the effects of travelling waves on water flow, though it neglects many factors present in a real-world scenario such as friction and turbulence.
Experimental Studies of Travelling-Wave-Induced Flows
Investigating travelling-wave-induced flows experimentally requires careful design and execution. The complexity of these flows, often involving multiple interacting physical phenomena, necessitates diverse experimental approaches tailored to the specific system under study. These studies provide crucial validation for theoretical models and offer insights into flow characteristics not readily accessible through simulations alone.Experimental setups vary greatly depending on the nature of the travelling wave and the system involved.
For instance, studying peristaltic pumping in microfluidic channels requires different techniques than investigating wave-induced flows in granular materials. Common approaches include using particle image velocimetry (PIV) to measure velocity fields, high-speed imaging to capture transient flow patterns, and various sensor arrays to measure pressure and other relevant parameters.
Experimental Setups and Techniques
A wide range of experimental techniques are employed to study travelling-wave-induced flows. In microfluidic systems, researchers often use transparent channels and micro-fabricated structures to generate controlled travelling waves, enabling direct visualization and precise measurements of flow velocities and pressure gradients using PIV or laser-induced fluorescence (LIF). For larger-scale systems, such as those involving surface waves or granular media, techniques like high-speed cameras and non-invasive flow measurement tools (e.g., ultrasonic Doppler velocimetry) are frequently used.
The choice of technique is driven by the scale of the system, the transparency of the medium, and the desired level of spatial and temporal resolution.
Examples of Experimental Data and Flow Characteristics
Experimental data often reveals complex flow patterns influenced by wave characteristics (frequency, amplitude, wavelength) and fluid properties (viscosity, density). For example, in peristaltic pumping, experiments show that flow rate is highly sensitive to wave speed and amplitude, exhibiting a non-linear relationship. Studies on wave-induced currents in shallow water demonstrate the formation of complex recirculation zones and the generation of secondary flows, with the strength of these flows directly correlated to wave height and frequency.
High-speed imaging might capture the development of vortices or separation bubbles, illustrating the transient nature of the flow. PIV data can quantify velocity fields, providing detailed information about the spatial distribution of flow velocities and revealing intricate flow structures.
Challenges and Limitations in Experimental Investigations
Experimental investigations of travelling-wave-induced flows present several challenges. Achieving precise control over wave parameters (amplitude, frequency, shape) can be difficult, especially in complex systems. Accurate measurement of flow fields in opaque or highly turbulent flows remains a significant hurdle. The high spatial and temporal resolution required to capture the fine details of these flows often necessitates sophisticated and expensive equipment.
Furthermore, scaling effects can complicate the extrapolation of experimental results to different scales or systems. For instance, results from a small-scale microfluidic experiment might not directly translate to a larger-scale industrial application.
Key Findings from a Published Study
The following is a summary of key findings from a hypothetical study (replace with a real published study and its data):
This section would contain a bulleted list summarizing key findings from a specific published study. For example:
- Increased wave amplitude resulted in a proportional increase in average flow velocity.
- A critical wave frequency was identified beyond which flow reversal occurred in specific regions.
- The presence of viscosity significantly dampened the flow response to the travelling wave.
- Numerical simulations showed good agreement with experimental measurements of velocity profiles, validating the chosen model.
- The study highlighted the importance of considering non-linear effects in modelling these flows at higher wave amplitudes.
Future Research Directions in Travelling-Wave-Induced Flows
The field of travelling-wave-induced flows, while having made significant strides, still presents numerous open questions and exciting avenues for future research. A deeper understanding of these flows is crucial for advancements in various applications, from microfluidics to geophysical processes. Further investigation will require a multidisciplinary approach, combining theoretical modelling, advanced experimental techniques, and high-performance computing.
Unresolved Aspects of Wave-Structure Interactions
Understanding the precise mechanisms governing the interaction between travelling waves and structures remains a significant challenge. Current models often simplify the wave-structure interaction, neglecting factors such as wave nonlinearity, three-dimensionality, and the complex rheology of the fluid. Future research should focus on developing more sophisticated computational models capable of accurately capturing these effects. This includes investigating the influence of boundary conditions and material properties on the flow characteristics.
For instance, the impact of surface roughness on wave attenuation and energy dissipation needs further investigation, particularly in applications involving porous media or complex geometries. A more comprehensive understanding will require incorporating advanced numerical techniques, such as Large Eddy Simulation (LES) and Direct Numerical Simulation (DNS), to resolve smaller scales of turbulence and accurately capture the complex flow dynamics.
Advancements in Experimental Techniques
The development of novel experimental techniques is crucial for validating theoretical models and gaining deeper insights into travelling-wave-induced flows. Advanced imaging techniques, such as high-speed Particle Image Velocimetry (PIV) and Micro-PIV, offer the potential to visualize and quantify flow fields with unprecedented detail. Furthermore, the use of advanced sensors and actuators allows for more precise control and measurement of the wave parameters and the resulting flow.
For example, integrating microfluidic devices with advanced optical techniques could enable detailed studies of wave-induced mixing and transport at the microscale. This would allow researchers to observe and quantify the subtle effects of wave parameters on the mixing efficiency in microfluidic channels, crucial for applications in lab-on-a-chip technologies.
Technological Advancements Facilitating Research
The increasing availability of high-performance computing resources opens new possibilities for simulating complex travelling-wave-induced flows. Advanced computational fluid dynamics (CFD) software, coupled with powerful parallel computing architectures, enables the simulation of larger and more realistic systems. Moreover, the development of artificial intelligence (AI) and machine learning (ML) techniques offers promising avenues for data analysis and model development. AI could be used to identify patterns and correlations in experimental data that may be missed by traditional methods, leading to the development of more accurate predictive models.
For example, machine learning algorithms could be trained on large datasets of experimental measurements to predict the flow characteristics under different wave conditions and geometrical configurations.
Hypothetical Experiment: Wave-Induced Mixing in a Microfluidic Channel
This experiment aims to investigate the efficiency of wave-induced mixing in a microfluidic channel with varying surface roughness. A microfluidic channel with controlled surface roughness (e.g., fabricated using micro-machining techniques) will be designed. A travelling surface wave will be generated using a piezoelectric actuator, and the resulting flow field will be visualized using Micro-PIV. Different wave frequencies and amplitudes will be tested, and the mixing efficiency will be quantified by tracking the dispersion of fluorescent dye injected into the channel.
The expected outcome is a quantitative relationship between wave parameters (frequency, amplitude), surface roughness, and mixing efficiency. This would provide valuable insights into the optimization of microfluidic mixers for various applications, such as drug delivery and biological assays. The data will then be used to validate and refine existing models of wave-induced mixing in microfluidic devices.
The study of travelling-wave-induced flows reveals a dynamic interplay between wave characteristics and fluid motion. We’ve journeyed from the foundational principles to the cutting-edge applications, highlighting the power of these flows in diverse scientific and engineering domains. Further research promises even deeper insights and innovative technological advancements based on this fundamental phenomenon.
Q&A: Travelling-wave-induced Flows
What are some real-world examples of travelling-wave-induced flows outside of the provided Artikel?
Examples include blood flow in arteries (due to pulse waves), peristaltic pumping in biological systems, and sediment transport in rivers.
How do the properties of the fluid (e.g., viscosity) affect travelling-wave-induced flows?
Viscosity significantly impacts flow patterns. Higher viscosity dampens flow velocities and reduces the influence of the travelling wave, leading to smoother, less pronounced flow structures.
What are the limitations of current mathematical models for these flows?
Current models often simplify complex interactions (like turbulence or multiphase flows). They may also struggle to accurately capture boundary effects or three-dimensional flow structures.
What are some emerging research areas in travelling-wave-induced flows?
Active research areas include exploring flows in complex geometries, investigating the impact of wave interactions, and developing advanced numerical methods for more accurate simulations.